Metoda pełzającego simpleksu Neldera-Meada

Metoda Neldera-Meada jest bezgradientową metodą minimalizacji bez ograniczeń n-wymiarowych funkcji . Simpleks w n-wymiarowej przestrzeni jest zbiorem n+1 punktów – wielościanem o n+1 wierzchołkach. Metoda sprawdza się dobrze nawet dla mocno nieliniowych funkcji jednak wymaga sporych nakładów pracy numerycznej szczególnie przy dużej liczbie zmiennych decyzyjnych. Dlatego zaleca się ją stosować dla funkcji celu mających nie więcej niż 10 wymiarów.

Oznaczenia:

x₀ – punkt startowy

d – początkowa odległość pomiędzy wierzchołkami simpleksu

α – współczynnik odbicia (α > 0)

β – współczynnik kontrakcji (0 < β < 1)

γ – współczynnik ekspansji (γ > 0)

ε – dokładność obliczeń

n – liczba zmiennych niezależnych

P_i – i-ty punkt simpleksu (i=1, 2, ..., n+1)

P_h – wybrany punkt simpleksu, w którym wartość funkcji osiąga największą wartość (najgorszy)

P_l – wybrany punkt simpleksu, w którym wartość funkcji osiąga najmniejszą wartość (najlepszy)

P' – środek symetrii simleksu liczony z wyłączeniem punktu P_h

Operacje:

• odbicie punktu P_h względem P'

  P^* = (1 + α) P' – αP_h

• ekspansja P^* względem P'

  P^** = (1 + γ) P^* – γP'

• kontrakcja punktu P_h względem P'

  P^*** = βP_h + (1 – β)P'

• redukja

  P_i = (P_i + P_l) / 2, i = 1, 2, ..., n+1

Algorytm:

1. Utworzenie simpleksu o n+1 wierzchołkach

2. Obliczenie wartości funkcji w punktach wierzchołkowych simleksu

   F_i = f(P_i), i = 1, 2, ..., n+1

3. Wyznaczenie h i l takich, że f(P_h) = max z wartości F_i, f(P_l) = min z F_i, dla i = 1, 2, ..., n+1

4. Obliczenie środka symetrii simpleksu z wyłączeniem punktu P_h

   

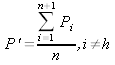
   oraz wartości funkcji F_s = f(P')

5. Odbicie P^* punktu P_h względem P' i obliczenie wartości funkcji F_o = f(P^*)

Jeżeli F_o < min, to:

6. Obliczenie P^** = (1 + γ) P^* – γP' i F_e = f(P^**)

   jeśli F_e < min, podstaw za P_h punkt P^**,

   jeśli F_e ≥ min, podstaw za P_h punkt P^*

7. O ile nie jest spełnione kryterium stopu, idź do kroku 2.

Jeżeli F_o > min, to:

8. Jeżeli F_o ≥ f(P_i) dla i = 1, 2, ..., n+1, i ≠ h

• jeśli F_o ≥ max, to idź do następnego kroku

• jeśli F_o < max, to podstaw za P_h punkt P^*

9. Wykonaj kontrakcję P^*** punktu P_h względem P' i oblicz F_k = f(P^***)

• jeżeli F_k ≥ max, to wykonaj redukcję simpleksu

• jeżeli F_k < max, to podstaw za P_h punkt P^*** i idź do kroku 11.

10. Jeżeli F_o < f(P_i) dla i = 1, 2, ..., n+1, i ≠ h, za P_h punkt P^*

11. Jeżeli warunek stopu nie jest spełniony, idź do kroku 2.

Warunek stopu może być sformułowany na kilka sposobów, np.:

• odległości pomiędzy wszystkimi punktami są mniejsze od ε

• odchylenie standardowe funkcji obliczonej w n+1 wierzchołkach simpleksu nie przekracza określonej wartości

  

Przykładowa trajektoria:

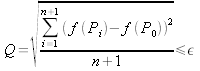
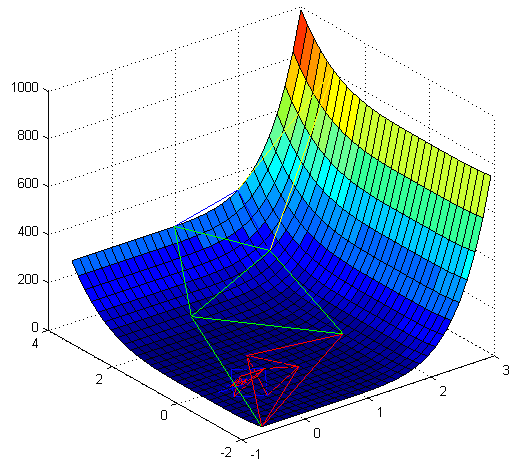
F(x, y) = x²+y², punkt początkowy (2, 3)

po 11 iteracjach znaleziono przybliżony pkt. minimalny: (-0,08, -0,07)

legenda: żółty -początkowy symplex, niebieski -odbicie, zielony -ekspansja, czerwony -kontrakcja